What AP Calculus Students Should Know for their Unit 3 Review
- merylsmagicmath

- Sep 23, 2024
- 3 min read
Updated: Jan 2, 2025
Need extra practice for your AP Calculus Unit 3 review? Outlined are the topics and derivative practice problems aligned with College Board’s curriculum to study for a Unit 3 test.
This unit adds to our derivative rule knowledge from Unit 2. It includes derivatives of composite, implicit, and inverse functions. Make sure you have all the rules memorized (making notecards is helpful!), and know when and how to apply them. These topics are often covered in multiple choice questions on the AP Calculus exam. Also, the derivative rules will continue to show up in Units 4 and 5, applications of derivatives.
As College Board outlines, the topics to review for Unit 3 are:
The Chain Rule
The chain rule is likely the most challenging rule for you so far. It can be difficult to see when it needs to be applied, there can be problems with multiple chain rules, and also problems with chain rules within product or quotient rules. Ultimately, the chain rule is used to take the derivative of a composition of functions, meaning a function within another function, such as f(g(x)). The derivative of f(g(x)) is f'(g(x))*g'(x). So you take the derivative of the outside function, keeping the inside function the same, then multiply by the derivative of the inside function.
If f(x)= sin(2x)+ln(x+1), then find f'(0)
Implicit Differentiation
Implicit differentiation is used for functions that have "y" embedded within the function. This is in contrast to other (explicit) derivative problems you've seen so far that have been y= or f(x)=...The key in solving these problems is that when you take the derivative of y, multiply by dy/dx or y'. This is because we want to take the derivative of each side with respect to x, so by multiplying the y derivative by dy/dx puts that term back with respect to x (instead of being with respect to y if you didn't multiply by dy/dx). I personally prefer to multiply by dy/dx instead of y' because it's easier to see the fraction dy/dx, which is what we're trying to solve for. Also, I want to make sure I know it's y prime and and not y to the first power.
3. What is the slope of the line tangent to the graph of ln(x+y)=x^2 at the point where x=1?
4. From the 2012 AP Calculus AB exam:
Differentiating Inverse Functions
You do not need to find the inverse function in order to take it's derivative. There is a formula to find the derivative of an inverse function. Many Calculus textbooks don't come right out and give the formula so I'll include it below.
5. From the 2012 AP Calculus AB exam:
Differentiating Inverse Trigonometric Functions
Make sure you have all 6 inverse trigonometric functions' derivatives memorized! They're often combined with chain rule.
6.
Selecting Procedures for Calculating Derivatives
This section is practice of Unit 2 and 3 problems combined, which I essentially did for the other practice problems, combining the chain rule with product and quotient rules. I'll include a table with derivative problems in order to look at questions from multiple perspectives.
7.
Calculating Higher-Order Derivatives
In higher-order derivatives, we take the derivative multiple times. Finding f'' is taking the derivative of f twice, or taking the derivative of y' or dy/dx.
8.
AP Calculus Unit 3 Review
For your AP Calculus Unit 3 review, make sure you are practicing derivative problems from multiple perspectives: given functions, tables, and graphs. If you need extra practice, check out the 8 best resources to study for AP Calculus tests. These resources have questions that match the rigor of your tests.
If you need further explanation on how to approach some of these difficult Unit 3 review questions, especially when all of the topics are mixed together, consider individual Calculus tutoring with me. I answer any questions students have, then provide practice solving my past test questions and previous AP exam questions. Getting more practice with problems given graphs, tables, and word problems will help you be prepared for in class tests and the AP exam.
Sign up for individual tutoring today!
Solutions to the above problems:
3
3.
4. A
5. D
6.
7.
8.
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.

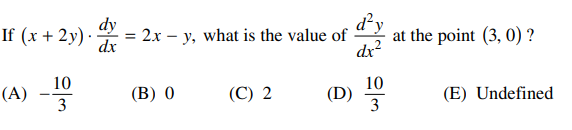
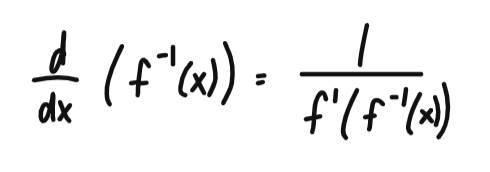





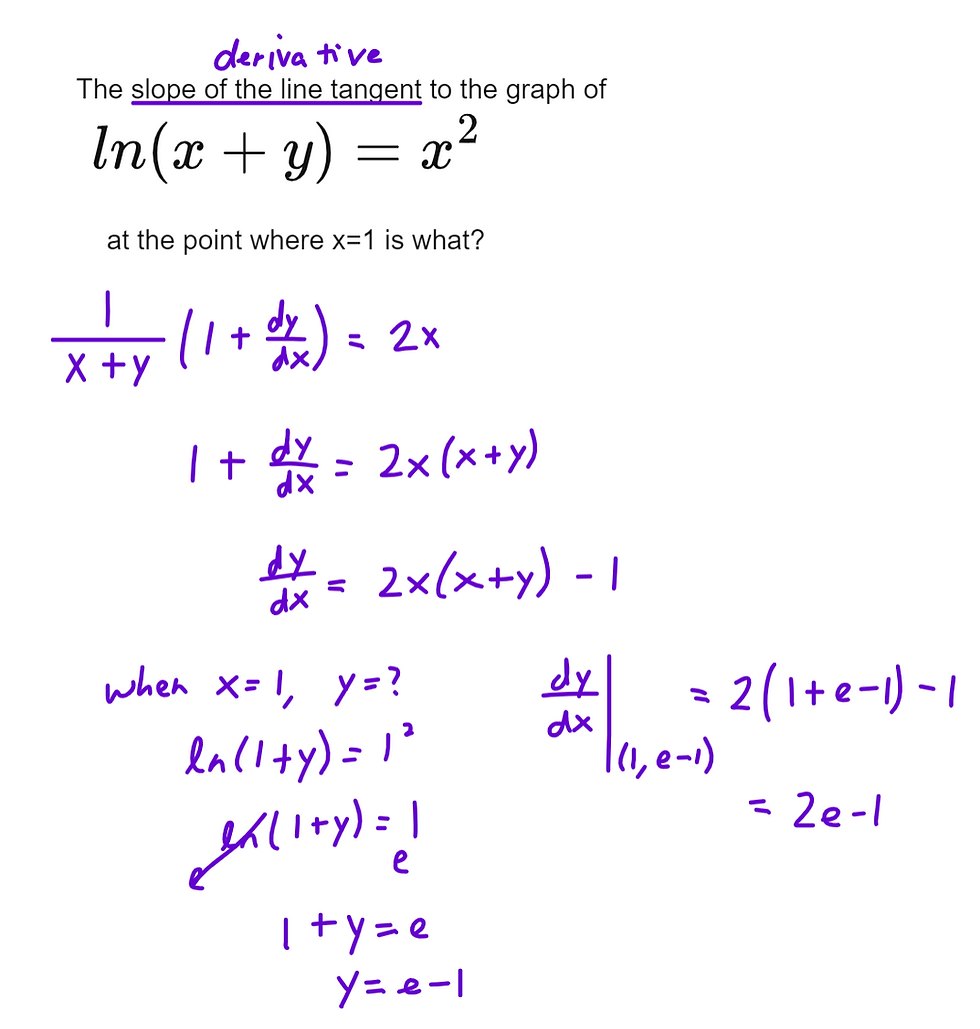

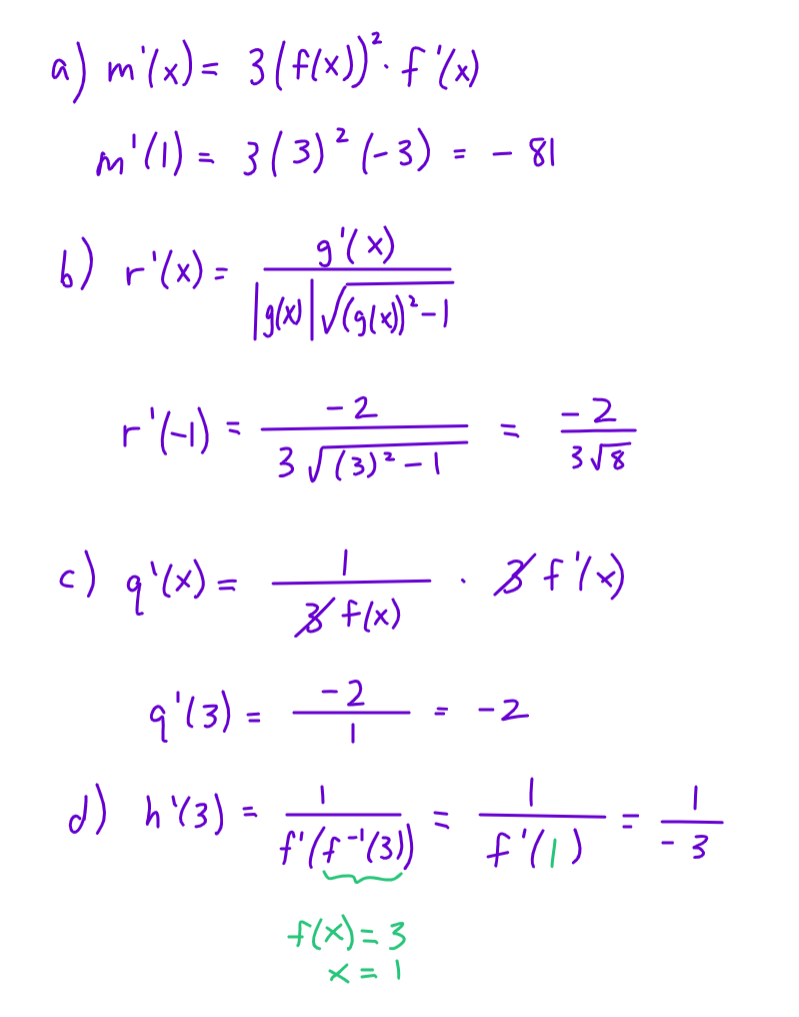




Comments