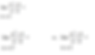What AP Calculus Students Should Know for their Unit 1 Review
- merylsmagicmath
- Aug 31, 2020
- 7 min read
Updated: Jan 27, 2025
Need extra practice for your AP Calculus Unit 1 review? Outlined are the topics and practice problems with limits and continuity, aligned with College Board’s curriculum, to study for a Unit 1 test. Follow these problems to reach your "limit" in the beginning of Calculus!
Limits and Continuity, the beginning unit of AP Calculus can be easy or difficult depending on your understanding of Algebra and Trigonometry from previous math courses. All of the Analytical approaches below rely on those key prerequisite skills.

As College Board outlines, the topics to review for Unit 1 are:
Introducing Calculus: Can Change Occur at an Instant?
This may not have been the first topic you covered this unit but it sets the stage for the importance of understanding word problems in AP Calculus. The first question on the AP Calculus free response portion is typically a word problem about a rate, and students are asked various questions about what the solution represents in the context of the problem.
This topic focuses on average and instantaneous rates of change, which is revisited in Unit 2. Make sure you're listing the time frame in your answer as well as units.
Try the problems below and check your solutions at the end!
Defining Limits and Using Limit Notation
A lot of this section could be combined with the next, evaluating limits from graphs. I'll leave that to the next section and just do a practice problem about limit notation:
2. Give an interpretation for
and does this mean that f(3)=7?
Estimating Limit Values from Graphs
Remember with limits, we're looking at the y-values the function approaches as we approach a given x-value. Sometimes we look at one-sided limits from either the left (-) or the right (+). If it's not a one sided limit, like with problem 2 above, we would need to check the y-values from both the left and the right of x=3 to ensure the y-values approach 7 from both sides. If the limits from the left and right don't match, the overall limit does not exist (DNE).
3.
Estimating Limit Values from Tables
Looking back to the graphic organizer at the beginning of the post, the numerical approach to limits is estimating limits given a table of values. Similar to graphs, we can look at one-sided limits or the overall limit would be from both sides. Recall, we're looking for the y or f(x) values as the x values get closer to the given number. We don't need to know the y-value at the exact given x-value, nor does the function need to be defined at that x-value!
4. Given the following table of values for y=f(x), estimate the given limit.
Determining Limits using Algebraic Properties
The biggest focus of this section would be evaluating limits given piecewise functions.
5.
Determining Limits using Algebraic Manipulation
Refer back to the graphic organizer to see all of the algebraic approaches to evaluating limits. This section looks at limits using direct substitution, factoring, and the special trigonometric limits (memorize those!). Always try direct substitution first. If it yields 0/0, that is indeterminate, so you'd have to try factoring or one of the other algebraic methods.
6.
Selecting Procedures for Determining Limits
The other algebraic approaches--rationalize/conjugate with radicals, common denominators with complex fractions, and absolute values are assessed here. But the other methods are also mixed in so make sure you know when to use which procedure.
7.
Determining Limits Using the Squeeze Theorem
Without fail, every student I tutor wants to focus on the Squeeze Theorem leading into their test on limits. It's understandable because there aren't many practice problems on it, so it doesn't fully make sense to students or they have a hard time determining when to use it. Ultimately, I would say don't worry too much about Squeeze Theorem. Sure, there may be 1 or 2 questions on your test, but it's not a major idea in AP Calculus, and it's not nearly as important as IVT or the algebraic methods to solving limits going into future units, or the AP exam. Check out several Squeeze Theorem questions. I snuck a practice Squeeze Theorem question into another section to see if you can recognize when to use it!
Exploring Types of Discontinuities
Discontinuity is a review of Pre-Calculus. Removable discontinuity is a hole on the graph, which algebraically is the result of the same factors cancelling out. Jump discontinuity comes from the left- and right-sided limits not matching, like in a piece-wise function. Infinite discontinuity is a vertical asymptote on the graph, which algebraically is the result of the denominator equaling 0 at that x-value. Oscillating discontinuity isn't too prevalent, but appears most commonly in trig functions that appear to approach multiple values at once like sin(1/x) at x=0.
8.
Defining Continuity at a Point and Removing Discontinuities
The formal definition of continuity at a point is:
It's worth noting, for the above problem, both of the expressions in the piecewise function are polynomials, and polynomials are continuous everywhere. The only x-value to worry about with discontinuity would be x=1, where the function switches from one expression to the other.
A common multiple choice question on the AP Calculus exam about continuity would be:
10.
Infinite Limits and Vertical Asymptotes
As mentioned above, vertical asymptotes occur at x-values where the function is undefined; specifically, where the denominator equals 0. If you try to evaluate a limit using direct substitution and get a number divided by 0, then a vertical asymptote occurs at that x-value. Picture a graph with a vertical asymptote. The graph either goes up to positive infinity, or down to negative infinity on either side of the vertical asymptote. Those are the only two possible answers for a one-sided limit at a vertical asymptote (the third possibility would be DNE for the overall limit if the one-sided limits don't match). What we have to do from there is evaluate the limit numerically, plugging in numbers just to the left and right of the x-value. For example, if we are looking at the limit as x approaches 3 and you've determined there's a vertical asymptote at x=3 since you got #/0 from direct substitution, you'd want to plug in something like 2.9, 2.99, or 2.999 from the left. Then, plug in 3.1, 3.01, or 3.001 from the right. Without a calculator, these calculations may be difficult (or at least take some time). The important thing is not getting the exact number, but looking at the signs of the result. Because the only possible options are positive or negative infinity. If you get +/+ or -/-, the answer is infinity. Getting +/- or -/+ results in negative infinity.
11.
Limits at Infinity and Horizontal Asymptotes
Horizontal asymptotes are the limits as x approaches positive or negative infinity. It's helpful to recall the horizontal asymptote rules from Pre-Calculus. Looking at the biggest powers, if the degree of the numerator is greater than the degree of the denominator, then there is no horizontal asymptote (so the limit would go to positive or negative infinity). If the degree of the numerator is the same as the degree of the denominator, then the horizontal asymptote/limit is the ratio of the coefficients of those biggest powers. If the degree of the numerator is less than the degree of the denominator, then the horizontal asymptote, and therefore limit, is 0. These rules apply for both limits approaching positive or negative infinity, but the only time the limit approaching infinity and negative infinity may not match is the first case where the degree of the numerator is greater than the degree of the denominator, or if there is an absolute value or square root in the expression.
12.
Intermediate Value Theorem (IVT)
First I'll explain Intermediate Value Theorem using a real-life example then showcase how it shows up on the AP Calculus exam. Let's say as a freshman, you were 5'2" and this year, as a senior, you're 5'8". At some point were you 5'7"? Yes! Since growth is continuous, at some time from freshman year to now, you were every height in between 5'2" and 5'8". IVT says for any continuous function from x=a to x=b, then the function takes on every y-value between f(a) and f(b) at some point in the interval. IVT appears a lot in the free response section of the AP Calculus exam, specifically with table prompts. Make sure that when you are applying IVT, you first discuss that the function is continuous! You won't earn points for your conclusion if you fail to mention the continuity condition is met (because then you can't technically apply IVT to the problem if the function isn't continuous).
13. From the 2022 AP Calculus exam,
AP Calculus Unit 1 Review
For your AP Calculus Unit 1 review, make sure you are practicing limit and continuity problems from multiple perspectives: given functions, tables, graphs, and word problems. If you need extra practice, check out the 7 best resources to study for AP Calculus tests. These resources have questions that match the rigor of your tests.
If you need further explanation on how to approach some of these difficult Unit 1 review questions, especially when all of the topics are mixed together, consider individual Calculus tutoring with me. I answer any questions students have, then provide practice solving my past test questions and previous AP exam questions. Getting more practice with problems given graphs, tables, and word problems will help you be prepared for in class tests and the AP exam.
Sign up for individual tutoring today!
Solutions to the problems above:
a) The number of students who sign up for the AP Calculus exam in 2020 b) The average rate of change in the number of students who sign up for the AP Calculus exam per year from 2015 to 2020. c) "The rate of students signing up for the AP Calculus exam per year in 2023." That is the most concise way of wording your answer. You could also say, "The instantaneous rate of change (in students per year) of the number of students who sign up for the AP Calculus exam in 2023"
As x approaches 3, the values of f(x) approach 7. This does NOT mean that f(3)=7. It is possible that f(3)=7 but not guaranteed.
4.
5.
6.
7.
8.
10.
11.
12.
13. Part (a) is technically in Unit 2, but you may be able to solve it from the first section of Unit 1.
AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.